The CAT Tab

This tab (Figure 4.7) includes options unique to a CAT.

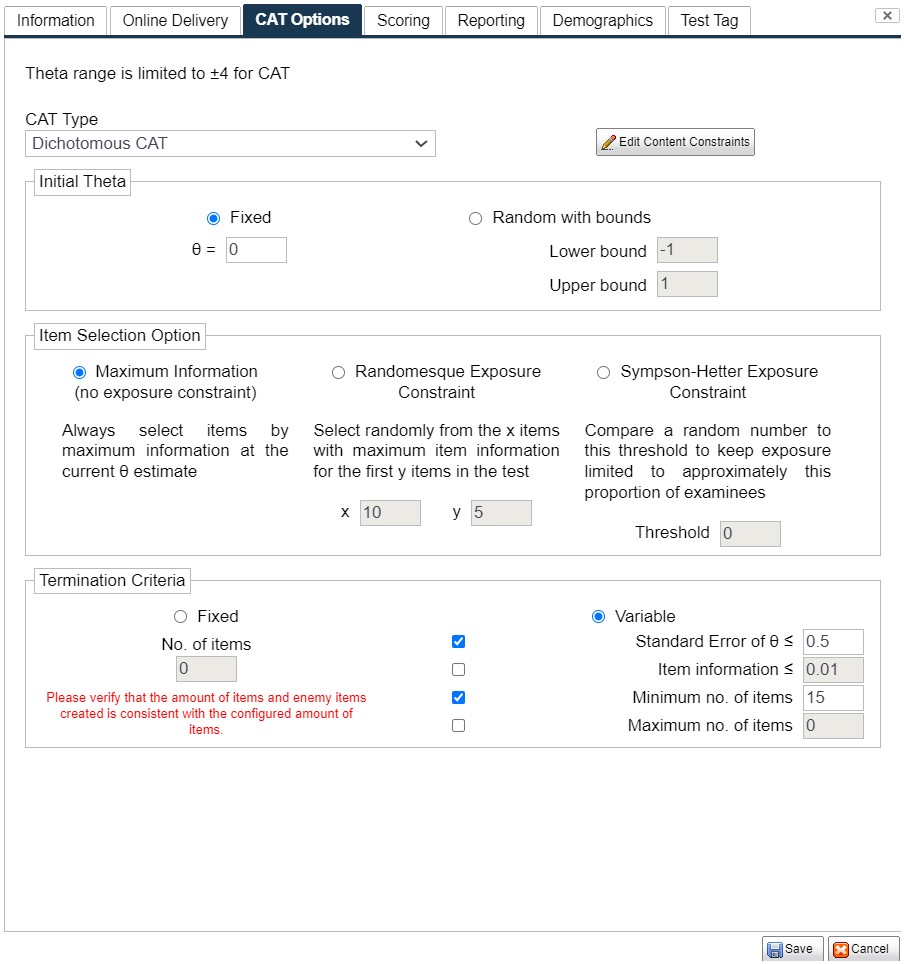
Figure 4.7: New Test Dialog – CAT Tab

CAT is a delivery method that uses IRT scoring to deliver items intelligently to each examinee.  The test adapts itself to each examinee, so that high-ability examinees do not waste time on easy items and low-ability examinees are not discouraged by difficult items.

• CAT requires the specification of 5 components (Thompson, 2010)

1. Item pool – a set of items calibrated with a psychometric model (e.g., IRT);
2. Initial θ (ability estimate) – where the algorithm should begin;
3. Item selection method – the process of matching items to examinee;
4. θ estimation method – the mathematical approach to determining based on responses to items that have been administered to an examinee;
5. Termination criterion – the mathematical and/or practical constraint that must be satisfied for an examinee’s test to end.

The item pool is defined by you in the process of developing the test in FastTest. This leaves the remaining four components to be specified.

Initial θ
CAT selects each item for an examinee individually by determining which item in the bank is most appropriate for their ability level. The ability level (θ) estimate is updated after each item.

• But for the first item, there is no θ estimate because no items have been administered yet – there is no way to score the examinee, so a temporary θ must be assigned.
• The simplest method is to assign every examinee to start at the same level, typically the average of the distribution, often θ = 0.0 (Option 1).
  • This has the drawback that every examinee will see the same first item unless there is randomization in the item selection (next paragraph).
  • A simple way to address this is to randomly pick an initial θ for each examinee within given bounds (Option 2).

Item Selection Method
A typical CAT adapts itself to each examinee by selecting the item with the most information at the current θ estimate (Option 1).

• This is the most efficient way to deliver items that are most appropriate for each examinee and obtain a precise final score with as few items as possible.
  • However, some testing programs wish to insert some amount of randomization (Option 2).
  • This randomization will, instead of picking the single item with the highest information, identify x number of items with the highest information, and randomly select between them.
  • This is extremely useful in two situations.
    • First, if the test is high-stakes and there is the possibility that the first few items will become well-known amongst examinees. Utilizing randomization will greatly increase the number of items being utilized across the population at the beginning of the test, aiding in security.
    • Second, if examinees will be taking the test more than once, the second test will likely lead down the same path into the bank; randomization will reduce the amount of items that are seen again during the second test.

θ Estimation Method
FastTest is designed to use maximum likelihood estimation (MLE) of θ. Because MLE is undefined for nonmixed response vectors early in a test, where examinees have all incorrect or all correct responses (always the case after the first item), Bayesian maximum a posteriori estimation (MAP) is utilized as a temporary θ estimation in those cases. The test reverts to the less biased MLE method which a mixed response vector is obtained (at least one correct and incorrect both).

Termination Criterion
There are two approaches to terminating the CAT:

1. Like conventional tests, a CAT can be ended after an arbitrary number of items that is the same for each examinee (e.g., 100 items for all examinees). This is Option 1.
   • However, the sophistication of CAT also allows for variable-length testing, where the test is concluded when a certain criterion is satisfied.
2. Option 2 has two choices.
   • First, you can end the test when the standard error of measurement (SEM) falls below a certain point. This ensures that all examinees have scores of equal precision, something which is nearly impossible with fixed-form conventional test.
   • The second choice is to end the test when no items remaining in the bank provide a certain level of information, which is designed to ensure that all items appropriate for a given examinee are used.

• Additionally, you can set a minimum and maximum for the test length. A minimum is useful to ensure that all examinees receive at least 20 items, for example. A maximum is intended to prevent the CAT from continuing until the entire item pool is used, which it will if either choice for Option 2 is too strict.

When a test is delivered via CAT, certain options are locked elsewhere in the Edit Test window.

• For example, the option of allowing examinees to mark items for review is disabled.
• Scoring is also fixed to IRT scoring. Concordantly, all scored items in a CAT must have an IRT model and parameters before the test can be protected.
• Unscored items (such as instructional and survey items) can also be placed in a CAT, but they will appear before and/or after the scored items.
  • To make unscored items appear before the scored items, place the unscored items adjacent as the first items in the test item list.
  • Any unscored item that is not grouped at the beginning of the item list, will appear at the end of the CAT.

Content Constraints
While computerized adaptive testing (CAT) is based on item response theory, which assumes an unidimensional trait, many testing applications have content areas or domains across which they desire to spread items.

• For example, a mathematics test might have a blueprint which calls for 75% algebra items and 25% geometry items.
  • When building a traditional fixed-form test, this can be explicitly controlled for; a 20-item test would have 15 algebra items and 5 geometry items.
  • CAT exam can be of variable length, so it needs to dynamically keep track of the item content distribution and select the next item appropriately.
    • If a CAT exam had delivered 19 items, 15 of which were algebra, then the CAT algorithm must know to select a geometry item next.

CATs implement this by constantly keeping track of the target proportions (0.75 and 0.25 in this example) and the actual proportions at any given time in the test.

• The target proportions are specified by the test designer based on the blueprint of the exam, in the Content Constraints dialog window of the CAT tab.
• Note that the exam pool must first be constructed according to the blueprints; that is, each item is specified as an algebra or geometry item.

Clicking the Edit Content Constraints button at the top of the CAT tab will bring up the following dialog. Note: this button only appears upon editing an existing test, not when creating a new test.

Figure 4.8: Content Constraints Dialog

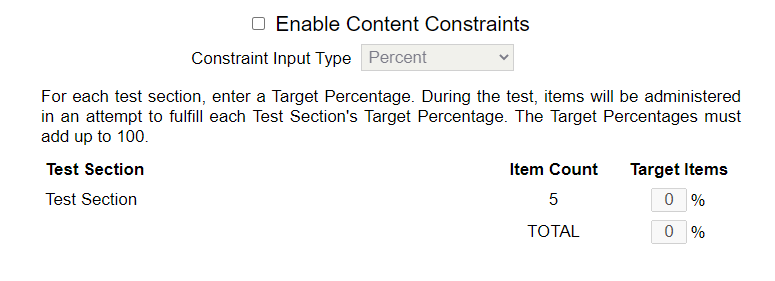
To enable Content Constraints, check the box at the top. The dialog lists all of the test sections defined for the test as well as the number of items in each test section. Each test section has an associated Target Percentage, which reflects the percentage of total items administered that should come from that section. The Target Percentages must add up to 100; you will be prevented from deleting a test section that has a positive Target Percentage assigned to it.